머신러닝 (편향과 분산)

Training data(학습 데이터) vs Test data(평가 데이터)

데이터의 분할

• 입력된 데이터는 학습 데이터와 평가 데이터로 나눌 수 있음
• 학습 데이터는 모델 학습에 사용되는 모든 데이터셋
• 평가 데이터는 오직 모델의 평가만을 위해 사용되는 데이터셋
• 평가 데이터는 절대로 모델 학습에 사용되면 안됨

평가 데이터

• 학습 데이터와 평가 데이터는 같은 분포를 가지는가?
• 평가 데이터는 어느 정도 크기를 가져야 하는가?

 

모델의 복잡도

• 선형에서 비선형 모델로 갈수록 복잡도가 증가함 -> 파라미터 수 증가
• 모델이 복잡해질수록, 학습 데이터를 더 완벽하게 학습함
• 그러면 좋은가? 

          1. 데이터가 많은 상황(Under - fitting)

          2. 데이터가 적은 상황(Over - fitting)

 

편향(bias)과 분산(variance)

• 편향과 분산은 모두 알고리즘이 가지고 있는 에러의 종류
• 편향은 under - fitting 과 관련 있는 개념
• 분산은 over-fitting 과 관련있는 개념

 

 

       선형                                                                    비선형

 

 

해결방안

일반적으로 모델의 복잡도를 키우고, 과적합을 막는 방법론을 사용

1. 검증 데이터셋을 활용
2. k-fold cross validation
3. 정규화 손실 함수

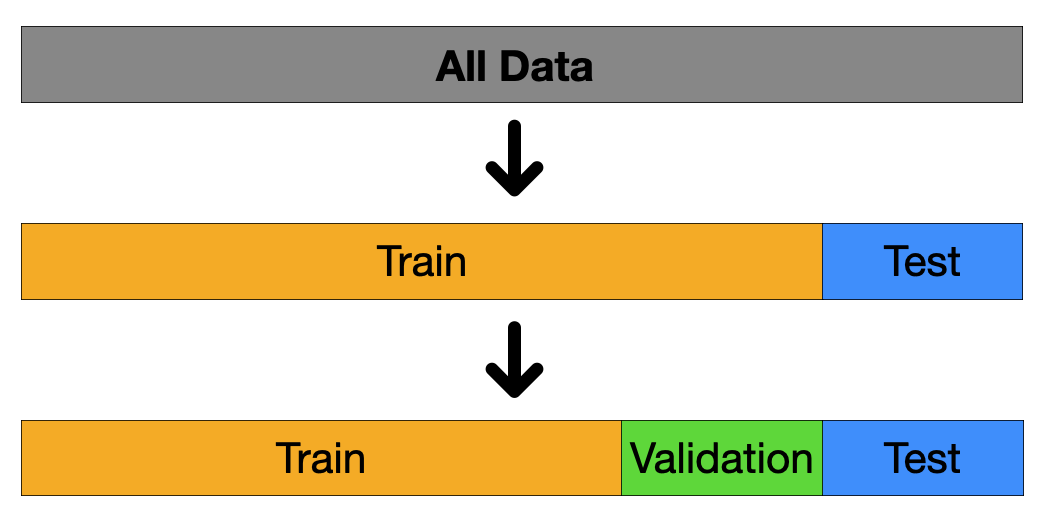
검증 데이터셋

• 모델 학습의 정도를 검증하기 위한 데이터셋
• 모델 학습에 직접적으로 참여하지 못함
• 학습 중간에 계속해서 평가를 하고, 가장좋은 성능의 파라미터를 저장해 둠

                                 80%                                                   10%                   10%

 

                                               학습 참여는 못하지만 검증은 가능

 

Leave - One - Out Cross - Validation

LOOCV

• 랜덤으로 생성된 검증 데이터셋 하나는 편향된 결과를 줄 수도 있음
• 검증 데이터셋에 포함된 샘플들은 모델이 학습할 수 없음
• 간단하게 모든 데이터 샘플에 대해서 검증을 진행할 수 있음

K-fold 교차 검즘

• LOOCV의 경우 계산 비용이 매우 큰 단점이 있음
• 이러한 문제를 해결하기 위해, K개의 파트로 나누어 검증을 진행하는 방법론
• Ex. 4-fold 교차검증

 

K의 값이 커지면  

1. 학습 데이터의 수는 커짐
2. Bias 에러값은 작고 Variance 에러값은 크다
3. 계산 비용은 커진다

 

 

Regularization

정규화된 손실 함수

• 모델의 복잡도가 커진다 == 모델의 파라미터 수가 많아진다
• 모델의 복잡도가 커질수록, 과적합(Over-fitting)이 발생할 가능성이 커진다
• 복잡도가 큰 모델을 정의하고, 그 중 중요한 파라미터만 학습하면 안될까?
• 필요없는 파라미터 값을 0으로 만들자

정규화 종류

• Ridge 회귀
• Lasso 회귀